PARTICIPANTS: DR. AMNAYA AWASTHI, MOHITH MANJUNATH (PHD), RAJ KUMAR PAL (PHD), KYLE SMITH (MS), PROF. JOHN LAMBROS (U. ILLINOIS), PROF. ALEX VAKAKIS (U. ILLINOIS), PROF. DAN TORTORELLI (U. ILLINOIS), PROF. TRUDY KRIVEN (U. ILLINOIS), PROF. CHIARA DARAIO (CALTECH) AND PROF. PHILIPPE GEUBELLE
SUPPORT: ARO MURI
PROJECT DESCRIPTION: In this project we investigate wave propagation characteristics of granular media. the dynamics of wave propagation chiefly depend upon the contact law of granular compression and this feature is being studied for devising wave tailored packaging applications. Our numerical studies for extended 2d granular media with elastic contacts have shown that for some configurations of material mismatch, 2d solitary waves propagate in the media whereas for some other configurations, the wave propagation occurs along straight lines. Research on granular chains consisting of randomness in material properties has shown that low randomness levels support solitary waves near the impact zone, however as randomness increases the solitary wave behavior decays quickly leading to dispersion effects which dominate propagation behavior. Solitary wave propagation is exponentially decaying while decay of the scatter follows a power law. Efforts are also underway to incorporate plasticity in the contact law with effects of material polydispersity and strain rates.

Another problem of interest pertains to the influence of randomness on wave propagation, which is unavoidable in any physical context. We study numerically 1d and 2D lattices of spherical particles where randomness occurs in mass, radius or elastic properties of the spheres. Randomness causes a gradual rearrangement of energy where potential energy is converted in kinetic. Following animation shows how randomness affects wave propagation in 1D.
View a video of a dynamic force response of a chain of spherical granules..
animation showing the dynamic force response of a chain of spherical granules where first 100 beads are identical (non-random) while remaining have randomness in mass. The peak force of the leading pulse attenuates leaving behind a scatter (noise) which eventually dominates the wave propagation
We re also involved with the development of more accurate force deformation laws to model granular contact to capture dissipation effects in granular media. One such effort is obtaining the contact law for elastoplastic materials. Utilizing the finite element technique, we have obtain the load displacement characteristics for contacts covering a wide range of material systems. View a typical force displacement simulation using abaqus.
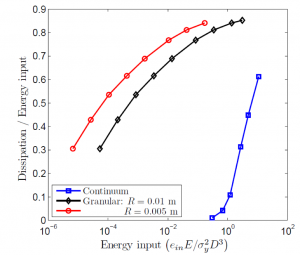
In this figure, we compare the energy dissipation properties of a continuum elasto-plastic medium to a granular medium made of the same material.
ADDITIONAL INFORMATION: More information about the project can be found at http://swami.cse.illinois.edu/.
PUBLICATIONS:
- Manjunath, M., Awasthi, A. P. and Geubelle, P. H. (2012) “Wave propagation in random granular chains.” Physical Review E, 86, 031308. DOI: http://dx.doi.org/10.1103/PhysRevE.85.031308.
- Awasthi, A., Smith, K., Geubelle, P. H. and Lambros, J. (2012) “Propagation of solitary waves in 2D granular media: a numerical study.” Mechanics of Materials, 54, 100-112. DOI: http://dx.doi.org/10.1016/j.mechmat.2012.07.005.
- Leonard, A., Daraio, C., Awasthi, A. and Geubelle, P. H. (2012) “Effect of weak disorder on stress-wave anisotropy in centered square nonlinear granular crystals.” Physical Review E, 86, 031305-1-10. DOI: http://dx.doi.org/10.1103/PhysRevE.86.031305.
- Pal, R. K., Awasthi, A. P., and Geubelle, P. H. (2013) “Wave propagation in elasto-plastic granular systems.” Granular Materials, 15:6, 747-758. DOI: http://dx.doi.org/10.1007/s10035-013-0449-1.
- Manjunath, M., Awasthi, A. P., and Geubelle, P. H. (2014) “Wave propagation in 2D random granular media.” Physica D: Nonlinear Phenomena, 266, 42-48. DOI: http://dx.doi.org/10.1016/j.physd.2013.10.004
- Manjunath, M., Awasthi, A. P., and Geubelle, P. H. (2014) “Plane wave propagation in 2D and 3D mono-disperse periodic granular media.” Granular Matter, 16:1, 141-150. DOI: http://dx.doi.org/10.1007/s10035-013-0475-z
- Pal, R. K., Awasthi, A, P. and Geubelle, P. H. (2014) “Characterization of wave propagation in elastic and elasto-plastic granular chains.” Physical Review E, 89, 012204-1 to 10. DOI: http://dx.doi.org/10.1103/PhysRevE.89.012204.
- Wang, E., Manjunath, M., Awasthi, A. P., Pal, R. K., Geubelle, P. H. and Lambros, J. (2014) “High-amplitude elastic solitary wave propagation in 1-D granular chains with preconditioned beads: experiments and theoretical analysis.” Journal of the Mechanics and Physics of Solids, 72, 161-173. http://dx.doi.org/10.1016/j.jmps.2014.08.002.
- Manjunath, M., Awasthi, A. P., and Geubelle, P. H. (2014) “Family of plane solitary waves in dimer granular crystals.” Physical Review E, 90, 032209. DOI: http://dx.doi.org/10.1103/PhysRevE.90.032209.
- Awasthi, A. P., Wang, Z., Broadhurst, N. R., and Geubelle, P. H. (2015) “Impact response of granular layers.” Granular Matter, 17(1), 21-31. DOI: http://dx.doi.org/10.1007/s10035-015-0547-3.
- Pal, R. K. and Geubelle, P. H. (2014) “Impact response of elasto-plastic granular and continuum systems: A comparative study.” Mechanics of Materials, 73, 38-50. http://dx.doi.org/10.1016/j.mechmat.2014.02.006.
- Pal, R. K., and Geubelle, P. H. (2014) “Wave tailoring by precompression in confined granular systems.” Physical Review E, 90, 042204. DOI:10.1103/Physreve.90.042204.
- Pal, R. K., Morton, J., Wang, E., Lambros, J., and Geubelle, P. H. (2014) “Impact response of elasto-plastic granular chains containing an intruder particle.” Journal of Applied Mechanics, 82:1, 011002. DOI: 10.1115/1.4028959.
- Pal, R. K., Waymel, R. F., Geubelle, P. H., and Lambros J. (2017) “Tunable wave propagation in granular crystals by altering lattice network topology.” Journal of Engineering Materials and Technology, 139, 011005-1-7. doi: 10.1115/1.4034820.
- MANJUNATH, Mohith (AE) Wave tailoring granular materials: effect of randomness and plane wave propagation. Ph. D. thesis. P. H. Geubelle, adviser (2014).
- PAL, Raj Kumar (TAM) Wave tailoring in elastic and elasto-plastic granular systems. Ph. D. thesis. P. H. Geubelle, adviser (2014).